Хроматический номер
«ОТ КРАЯ И ДО КРАЯ...» — эти слова из песни несут в себе, как видите, глубокий топологический смысл. Лист бумаги — модель двусторонней односвязной (число Бетти равно единице) поверхности с одним краем. Его можно смять и бросить в урну, но все равно число краев (и сторон) останется прежним. Но у сферы краев нет. Нет их и у тора — говоря попросту, бублика. Зато нарисованное на бумаге кольцо имеет целых два края. Один край и у мебиусова листа, как одна у него и сторона. И снова — сделайте его из какой угодно эластичной резины и растяните до любых размеров — топологические свойства, этот незыблемый фундамент самого естества геометрической фигуры, останутся неизменными.
Не много ли неожиданных и странных свойств? Тогда еще только два, быть может, самых любопытных. Первое — ориентированность. Конечно, можно было бы подробно рассказать, что это такое. Но лучше дать определение «от противного»: это то, чего нет у листа Мебиуса! Вообразите, что в нем заключен целый плоский мир, где есть только два измерения, а его обитатели — несимметричные рожицы, не имеющие, как и сам лист, никакой толщины. Если эти несчастные создания пропутешествуют по всем изгибам листа Мебиуса и вернутся в родные пенаты, то с изумлением обнаружат, что превратились в свое собственное зеркальное отображение. Конечно, все это случится только, если они живут в листе, а не на нем.
Впрочем, это удивительное явление можно наблюдать и на действующей модели плоского мира Мебиуса — для этого надо сделать ленту из любого прозрачного материала.
И наконец, то, что носит название «хроматический номер». Он равен максимальному числу областей, которые можно нарисовать на поверхности так, чтобы каждая из них имела общую границу со всеми другими. Если каждую такую область выкрасить по-разному, то любой цвет должен соседствовать с любым другим. Так вот, на листке бумаги, даже если его склеить в кольцо, еще никому не удалось расположить пять цветных пятен любой формы, которые имели бы всеобщую границу. И на сфере, и на цилиндре их может быть не более четырех. Это и значит, что хроматический номер этих поверхностей — четыре. А на бублике число соседствующих цветов равняется семи. Каков же хроматический номер листа Мебиуса? Он, как это ни поразительно, равен шести.
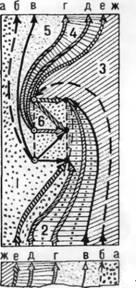
Конечно же, такое не укладывается в голове. Ну в самом деле, не довольно ли этих мебиусовских мистификаций? Видите ли, на ленте, склеенной, как положено, размещается всего четыре цвета, а стоит соединить ее концы шиворот-навыворот — и непонятно, как находится место еще для двух цветов! Но клин выбивают клином, одну головоломку — другой. Есть древняя неразрешимая задача. Надо соединить три дома с тремя колодцами, но так, чтобы жители каждого из домов могли ходить по воду в любой колодец и при этом пути их нигде не пересекались. Сделать это не умудрился никто, но лишь сравнительно недавно математики строго доказали, что задача неразрешима. (Неразрешима на плоскости, а на торе, то есть бублике, например, все получается просто.) А теперь взгляните на рисунок. Если склеить эту полоску бумаги так, чтобы совпали одинаковые буквы на ее краях, то проблема водоснабжения решается. Разумеется, вы снова получите все тот же лист Мебиуса. А теперь раскрасьте карту путей водовозов — и вот вам шесть цветов, живущих в дружном соседстве. Но, конечно, как и раньше, надо предполагать, что все события происходят не на листе, а внутри него. Иными словами, краски должны проникать сквозь бумагу, как чернила сквозь промокашку.
И напоследок возьмите еще раз в руки лист Мебиуса — одностороннюю неориентированную поверхность с одним краем, числом Бетти, равным двум, и хроматическим номером, равным шести. Этот листок бумаги открыл математикам мир новых возможностей, а вам доставил несколько приятных минут. Но не спешите с благодарностью прощаться с ним. Он нам еще встретится — в космических далях Вселенной.
...У Фридриха Дюрренматта, в его нашумевшей в свое время пьесе «Физики», трое абсолютно здоровых ученых сознательно изображают из себя сумасшедших. Весь персонал дома умалишенных обращается к ним не иначе, как «господин Ньютон», «господин Эйнштейн» и «господин Мебиус». Разумеется, фантазия драматурга могла поместить в столь экзотические обстоятельства и других каких-либо прославленных ученых — тем более, что Мебиус не такой уж физик, каким он, видимо, казался Дюрренматту. И все-таки выбор его не выглядит случайным. Вселенная Эйнштейна сменила вселенную Ньютона благодаря тому, что удалось постичь некую глубокую внутреннюю закономерность, свойственную природе. Вселенная Мебиуса... Нет, конечно, ее не было, нет и, наверное, не будет. Но мебиусианские идеи касаются настолько интимных свойств нашего мира, что они просто не имеют права как-то не проявить себя в грядущих фундаментальных исследованиях.