Гость из четвертого измерения
Представители двумерного мира имеют и длину и ширину — это ленты, куски ткани, листы бумаги. Окружность, граница двумерного круга — вот что такое сфера в пространстве двух измерений.
И наконец, кубы, пирамиды, дома, корабли и самолеты, так же, как и мы с вами, входят в неисчислимую армию «трехмерцев», обладающих вдобавок к длине и ширине еще и высотой. У них есть объем. Сфера в трехмерном пространстве — это шар, «обычная» сфера.
Но вот что любопытно. Проволоку можно сломать, лист бумаги разрезать, а куб распилить. И при этом получается, что одномерная поверхность — линия — разделяется поверхностью нулевого измерения — точкой. Двумерная плоскость делится надвое одномерной линией, а трехмерный куб — двумерной плоскостью. Иными словами, границей «разлома» тела служит какое-то другое тело, измерение которого на единицу ниже.
Что же тогда служит границей четырехмерной сферы? Поистине, прав Эйнштейн — оторопь берет, когда пытаешься все это вообразить! Но не будем отчаиваться и зайдем с другого конца.
Если точку «протащить» по бумаге, то получится линия. Линия, в свою очередь, «заметает» плоскость — получается квадрат. Вытянем квадрат из плоскости — сделаем куб. Это уже третье измерение. Но что же такое надо сделать с кубом, чтобы обратить его в четырехмерное тело? И как его себе представить?
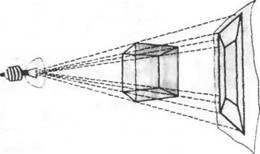
А что мы делаем, чтобы изобразить на плоском листе бумаги трехмерный куб? Мы проецируем его на плоскость. Получаются два квадрата один в другом, соединенные вершинами. Так спроецируем же и четырехмерный куб! Мы получим по аналогии два куба, один в другом, и снова вершины попарно соединены. Вот он, посланец четвертого измерения, вернее, не сам он, а его проекция на плоскость.
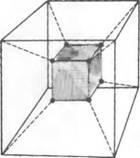
И точно так же, рассуждая по аналогии, мы можем отдаленно представить себе четырехмерную сферу. Если спроецировать глобус на плоскость, то проекции двух его половин наложатся одна на другую, и Нью-Йорк окажется где-то в центре нашей Сибири. Проецируя глобус, мы пропустим одну его полусферу сквозь другую и соединим их проекции — круги — только по границе — окружности (как квадраты по вершинам). Проекция гиперсферы — два шара, прошедшие один через другой и соединенные только по внешним поверхностям. Конечно, вообразить все это нелегко, но ничего мистического тут нет.