Вероятностные методы
Для решения вопросов такого рода и применяются вероятностные методы, методы, которые не говорят точно, сколько, но позволяют с достаточной точностью определить, в каких пределах будет изменяться искомая величина, или с какой вероятностью можно ожидать какого-либо события.
Один из таких методов и назван методом Монте-Карло. Для того чтобы понять сущность его, рассмотрим несложный пример.
Пусть требуется определить площадь круга, радиус которого равен 1 см. Эта площадь, как известно, равна п = 3,14 см2, т. е. равна числу п.
А задумывался ли читатель, как можно определить число п? Это довольно просто можно сделать методом Монте-Карло.
Будем много раз бросать песчинку на лист бумаги, покрытый кругами радиусом 1 см, расположенными плотными рядами (рис. 1). Песчинка будет падать либо в один из кружков, либо в пустоты между ними. Чем больше площадь, занятая кружками, тем чаще песчинка попадает в кружок. Пусть вся площадь квадрата равна 10 см2 и пусть из 1000 бросаний песчинка 700 раз остановилась на кружках и 300 раз на пустотах. Тогда можно полагать, что кружки занимают частей площади, т. е. 7 см2.
Ясно, что таким способом можно вычислить площадь одного кружка, а следовательно, и получить число п. Для этого достаточно площадь всех кружков разделить на их количество. Как легко заметить, такой эксперимент займет довольно много времени. Очевидно, результат будет тем точнее, чем большее число раз мы будем бросать песчинку.
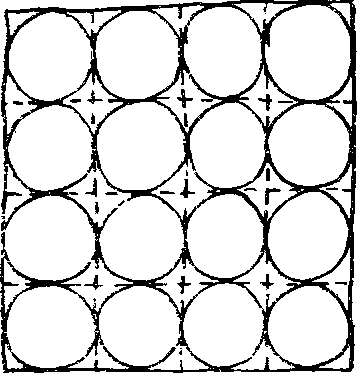
Рис. 1. Попробуйте бросать песчинку на этот рисунок и считать, сколько раз она попадет в один из кружков. Если набраться терпения и проделать этот эксперимент много раз. то можно вычислить таким образом площадь, занимаемую всеми кружками.
- Материалы
Поцелуй по расчету
Поэма Содди
Задача о сферах
Многомерность
Гость из четвертого измерения
Четырехмерный симплекс
Возможности нового измерения
Эксперимент Цельнера
Геометрия - это интуиция
Ущербность нашего восприятия
Объем - в плоскость
Наш плоский объемный мир
Мебиусиана
Односторонность листа Мебиуса
Топология - из листа Мебиуса
Число Бетти
Хроматический номер
Справа, где сердце
Бутылка Клейна
Мебиус и микромир
Левый и Правый Мебиусы
Эксперимент By Цзянь-сюн
Двухкомпонентная теория нейтрино
Зеркальные двойники
Роль формы
Вселенная искривляется
Тензорный анализ
Теория Вселенной Эйнштейна
Пульс Вселенной
Великолепная пятерка
О божественной пропорции
«Начала» Евклида
Доказательство Эйлера
Символы Шлефли
Гамильтонова линия
Изопиранная задача
Интуиция царицы Дидоны
Как управляется мир
Серьезные игры
Искусство орнамента
Федоровские группы
Игры Эсхера
Симметрии Эсхера
Нефедоровская кристаллография
Мировая гармония
Удавшаяся провокация
«Колючий» ёж Кеплера
Фигура Петри
Теория многогранников
Правильные и почти правильные тела
Песок расширяется!
Кубическая плотная упаковка
Плотность упаковки
Дома на песке
Тайные связи
Музыка сфер
Подкупающая простота
Модели Дончияна
Полезные политопы
Организация пространства
Радость видеть и понимать
Теории Земли
Бейсбольный мяч планеты
Катенаны
Вечный Геометр
Цепь причин и следствий
Счастливый случай
Метод Монте-Карло
Вероятностные методы
Бросаем песчинку
Сходство схем
Задачи распространения тепла
Случайные траектории
Возможности равны
Случай в игре
Игры с таблицей
Новые осложнения
Хуже-лучше
Расшифровка кодов
Роль элемента случайности
Обучение и случайность
Обучение автоматов
«Школьная» схема обучения
Обучение — самообучение
Шаблон поведения
Уметь пользоваться памятью
Опыты И. П. Павлова
Условный рефлекс
Связь между нейронами
Носитель памяти
Механизм образования условного рефлекса
Механизм «вспоминания»
Структура нервной сети
Простой эксперимент
Проблема опознания
Что такое опознание
Зрительные образы
Персептрон
Различаемые образы
Что умеет персептрон
Свойства персептрона
Залог опознания образов
Роль случайности в эволюции
К чему приводят мутации
Естественный отбор
«Безжалостность» законов природы
Приспособление вида
Схема гомеостата
Идея Эшби
Усилитель отбора
Усилитель мыслительных способностей
Схема искусственного отбора
Самонастраивающиеся системы и случайность
Непохожесть систем
Критерий близости к совершенству
Самонастраивающиеся системы
Наладчик сложных систем
Метод компенсации
Как настроить
Устройство автомата
Держим точный размер
Анализ станка-автомата
Обратное воздействие
Способ Гаусса — Зейделя
Анализ настроек
Метод градиента
Метод случайной настройки
Метод случайного поиска
Программа случайного поиска
Схема случайного поиска
Самонастраивающаяся система
Источник неограниченных возможностей