Мировая гармония

Рано или поздно всякая правильная математическая идея находила применение в том или ином деле.
Алексей Николаевич КРЫЛОВ
«СИММЕТРИЯ... ОХВАТЫВАЕТ СВОЙСТВА ВСЕХ ФИЗИЧЕСКИХ ПОЛЕЙ, С КОТОРЫМИ ИМЕЮТ ДЕЛО ФИЗИК И ХИМИК», — считал академик Владимир Иванович Вернадский. Но если уж речь идет о физике и химике, то что говорить о математике?
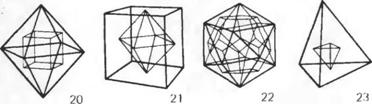
Правильные геометрические мозаики, истинные образцы симметрии, как мы имели удовольствие убедиться, двойственны в том смысле, что центры составляющих их фигур служат вершинами для других фигур. И точно так же дело обстоит у правильных многогранников, только их в этом случае называют взаимными. Октаэдр, например, взаимен кубу ( «Среди правильных тел самое первое, начало и родитель остальных — куб, а его, если позволительно так сказать, супруга — октаэдр, ибо у октаэдра столько углов, сколько у куба граней», — писал Кеплер. Это видно и на гравюре Эсхера «Кристалл».) (20, 21), икосаэдр — додекаэдру (22), а вот тетраэдр взаимен сам себе (23), как квадратная мозаика тоже сама себе двойственна. Об этом говорит и симметрия символов Шлефли — {4,3} и {3,4} у куба и октаэдра, {3,5} и {5,3} — у икосаэдра и додекаэдра, {3,3} — у тетраэдра и {4,4} — у квадратной мозаики.
Именно поэтому родственные мозаики и многогранники изящнейшим образом вписываются друг в друга.
Но вот что настораживает. Два тетраэдра, прошедших один сквозь другой, образуют восьмигранник — вы увидите его в правом верхнем углу гравюры Маурица Эсхера «Звезды» ( На этой же гравюре внимательный глаз различит и все правильные многогранники. В частности, нижний хамелеон держится передними лапами за октаэдр и тетраэдр, а хвостом обвил другой октаэдр. Верхняя же тварь, наоборот, обвила хвостом ребро тетраэдра, а лапами вцепилась в два октаэдра. ). (Эскиз к ней — на первой странице обложки, там эта фигура, наоборот, в левом нижнем углу, а раньше она встречалась нам в виде гравюры «Двойной планетоид».) Лука Пачоли, первым обнаруживший эту фигуру, назвал ее «продолженным октаэдром», а его великий друг Леонадро да Винчи сделал соответствующий деревянный каркас, перерисовав его затем в их общую книгу «О божественной пропорции». «Octacedron eleva - tus soudus», то есть «продолженный октаэдр сплошной», — написано там его рукой. Иоганн Кеплер переоткрыл эту фигуру сто лет спустя и присвоил ей имя «Стелла октангула» — «восьмиугольная звезда». Она встречается и в природе: это так называемый двойной кристалл. Но она же перечеркивает все, что было сказано до сих пор! Мы вынуждены признать «стеллу октангулу» правильным многогранником: ведь все ее грани — правильные треугольники одинакового размера и все углы между ними равны!
- Материалы
Поцелуй по расчету
Поэма Содди
Задача о сферах
Многомерность
Гость из четвертого измерения
Четырехмерный симплекс
Возможности нового измерения
Эксперимент Цельнера
Геометрия - это интуиция
Ущербность нашего восприятия
Объем - в плоскость
Наш плоский объемный мир
Мебиусиана
Односторонность листа Мебиуса
Топология - из листа Мебиуса
Число Бетти
Хроматический номер
Справа, где сердце
Бутылка Клейна
Мебиус и микромир
Левый и Правый Мебиусы
Эксперимент By Цзянь-сюн
Двухкомпонентная теория нейтрино
Зеркальные двойники
Роль формы
Вселенная искривляется
Тензорный анализ
Теория Вселенной Эйнштейна
Пульс Вселенной
Великолепная пятерка
О божественной пропорции
«Начала» Евклида
Доказательство Эйлера
Символы Шлефли
Гамильтонова линия
Изопиранная задача
Интуиция царицы Дидоны
Как управляется мир
Серьезные игры
Искусство орнамента
Федоровские группы
Игры Эсхера
Симметрии Эсхера
Нефедоровская кристаллография
Мировая гармония
Удавшаяся провокация
«Колючий» ёж Кеплера
Фигура Петри
Теория многогранников
Правильные и почти правильные тела
Песок расширяется!
Кубическая плотная упаковка
Плотность упаковки
Дома на песке
Тайные связи
Музыка сфер
Подкупающая простота
Модели Дончияна
Полезные политопы
Организация пространства
Радость видеть и понимать
Теории Земли
Бейсбольный мяч планеты
Катенаны
Вечный Геометр
Цепь причин и следствий
Счастливый случай
Метод Монте-Карло
Вероятностные методы
Бросаем песчинку
Сходство схем
Задачи распространения тепла
Случайные траектории
Возможности равны
Случай в игре
Игры с таблицей
Новые осложнения
Хуже-лучше
Расшифровка кодов
Роль элемента случайности
Обучение и случайность
Обучение автоматов
«Школьная» схема обучения
Обучение — самообучение
Шаблон поведения
Уметь пользоваться памятью
Опыты И. П. Павлова
Условный рефлекс
Связь между нейронами
Носитель памяти
Механизм образования условного рефлекса
Механизм «вспоминания»
Структура нервной сети
Простой эксперимент
Проблема опознания
Что такое опознание
Зрительные образы
Персептрон
Различаемые образы
Что умеет персептрон
Свойства персептрона
Залог опознания образов
Роль случайности в эволюции
К чему приводят мутации
Естественный отбор
«Безжалостность» законов природы
Приспособление вида
Схема гомеостата
Идея Эшби
Усилитель отбора
Усилитель мыслительных способностей
Схема искусственного отбора
Самонастраивающиеся системы и случайность
Непохожесть систем
Критерий близости к совершенству
Самонастраивающиеся системы
Наладчик сложных систем
Метод компенсации
Как настроить
Устройство автомата
Держим точный размер
Анализ станка-автомата
Обратное воздействие
Способ Гаусса — Зейделя
Анализ настроек
Метод градиента
Метод случайной настройки
Метод случайного поиска
Программа случайного поиска
Схема случайного поиска
Самонастраивающаяся система
Источник неограниченных возможностей